
Structures given are primitive cubic packing, primitive hexagonal packing, face-centered-cubic close-packing, hexagonal close-packing, body-centered packing, CsCl, diamond, zinc blende, CaF2, ReO3, perovskite, NaCl, Mg3NF3, SiO2, Cu3Au, NiAs, wurtzite, and graphite.

In the case of intricate structures, the pedagogical interest lies in the possibility of describing the whole structure as the sum of very simple partial structures, each corresponding to a part of the equation. The generated surface is aligned in the XY plane, and a specified thickness will be cleaved in the z-axis below the XY plane. The Figure below illustrates the relationship of a unit cell to the entire crystal lattice. A crystal can be thought of as the same unit cell repeated over and over in three dimensions. Plotting the equations gives the classical ball representation of the structures. Specify the indices of the Miller plane desired (for hexagonal unit cells, all 4 indices will appear), and choose the dimensions in either distances or repeating cells of the resulting surface. A unit cell is the smallest portion of a crystal lattice that shows the three-dimensional pattern of the entire crystal. exposed for no longer than twenty minutes, so the experiment was repeated for. A number of fundamental crystal structures are described as mathematical functions. 4.10 Zn1xMnxSe unit cells for modeled (a) CuPt A (111) and (b) CuPt. Repeat steps 24, but requesting MgO bonds. In this type of unit cell: the coordination number is 6, there is 1 atom per cell, and the length of the edge of a cell is equal to 2 r. The simplest unit cell is the primitive cubic unit cell in which there are atoms at each of the 8 corners of a cube. Using mathematics from the method of the exponential scale, crystals inner and outer structures are given. This is because CrystalMaker can use any symmetry (including lattice translations) to build a complete unit. A unit cell is the simplest repeating unit of a crystalline solid.
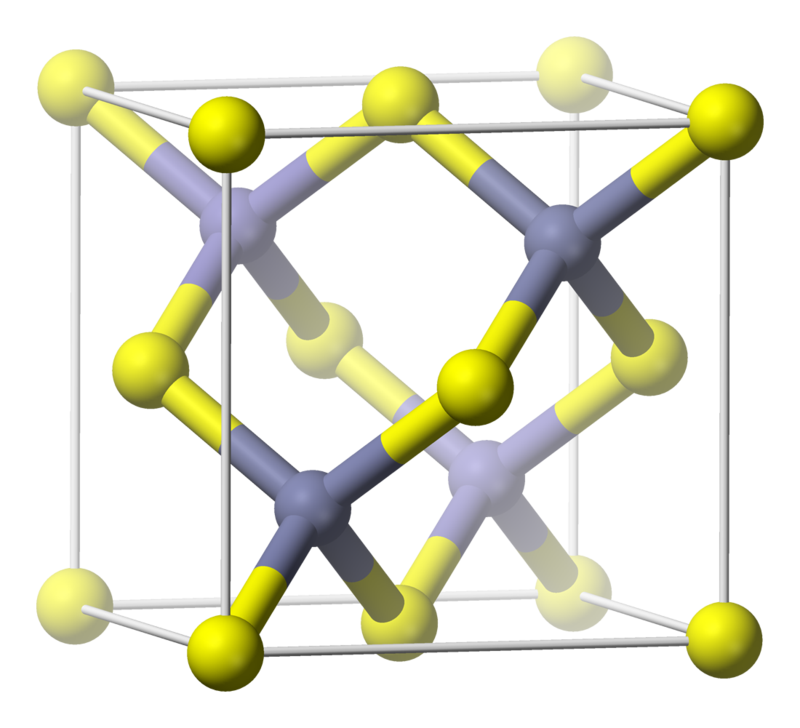
Teaching Crystal Structures with 3–D Surfaces Teaching Crystal Structures with 3–D Surfaces


 0 kommentar(er)
0 kommentar(er)
